A student’s test score is only meaningful in relation to something else – 1) information on the performance of a particular group of students, 2) some pre-established standard of performance, 3) a test score reflecting previous performance of the student, or 4) a prediction of performance based on previous testing. The last two of these, of course, get at the idea of student academic growth. The reporting of student growth has become a must for testing programs and companies even though there are many reasons to be leery of individual student growth scores.
Simple Growth
What could be easier to understand than “simple growth,” Test 2 score minus Test 1 score? Yet I’ve seen district programs that compute growth in this manner when there has been little or no effort to assure that the two tests cover the same material or that they are of equal difficulty. In such a case, a totally meaningless growth score is treated as if it is a true indicator of how much a student has learned. Interestingly, even if those two requirements for measuring growth are met, there are still problems with the results. One of the first things educators used to learn about testing is that “change scores are unreliable.” Even with high quality, equated pre-tests and post-tests, because there is measurement error associated with each test, error is compounded when one score is subtracted from the other. That is, the score difference has much more measurement error than either of the two tests themselves.
Short-term Growth
Even with equated tests, there are other issues. I heard of one district administering commercial general achievement measures in reading and math four or five times during the course of a school year. With short time spans between administrations, expected growth during any one interval would be minimal. And because measurement error could overshadow such limited growth, there could be individual students whose results would falsely indicate negative growth. Even adding growth scores across the short time intervals could suggest negative growth for some students. The difference between end-of-year and beginning-of-year scores would be more appropriate to compute. This is the growth of interest in state accountability systems. One interim measure would be reasonable to administer for purposes of “early warning” – that is, the identification of students or curricular areas requiring additional attention before end-of-year accountability testing, even if the identification of the first is less than perfect.
Grade Equivalent Scores and Vertical Scales
A grade equivalent is represented by a decimal numeral, with the digit(s) to the left of the decimal point indicating a grade in school and the digit(s) to the right of the decimal point indicating a month within the school year. A student achieving a score of 5.4 has performed the same as a typical student performs at the end of the fourth month in the fifth grade in school. If the student earned that score when tested at the end of the school year when the typical student scores 5.8, one has a sense of how far “behind” the student is.
One of the problems with grade equivalent scores is that it is quite frequent that students achieve a grade equivalent that is “out of grade.” Inevitably, parents whose fourth grader earns a 6.3 grade equivalent on a test believes their child should be able to skip grades. Yet the student has not even been exposed to sixth grade concepts and skills! Additionally, the parts of grade equivalents representing years and months, these scores cannot be subtracted or averaged meaningfully.
The commercial tests reporting grade equivalents have been vertically scaled. That means that in developing the test series, the company included “overlap” items in their pilot or scaling tests for different grades – for example, the fourth grade test included some third grade items and some fifth grade items. These linkages between adjacent grades’ tests allowed the companies to produce a giant “vertical scale” to which all students’ scores belonged, regardless of grade. In recent years, grade equivalent scores have been de-emphasized, with scores on the vertical scales getting more attention. No digit in a scaled score indicates a grade level.
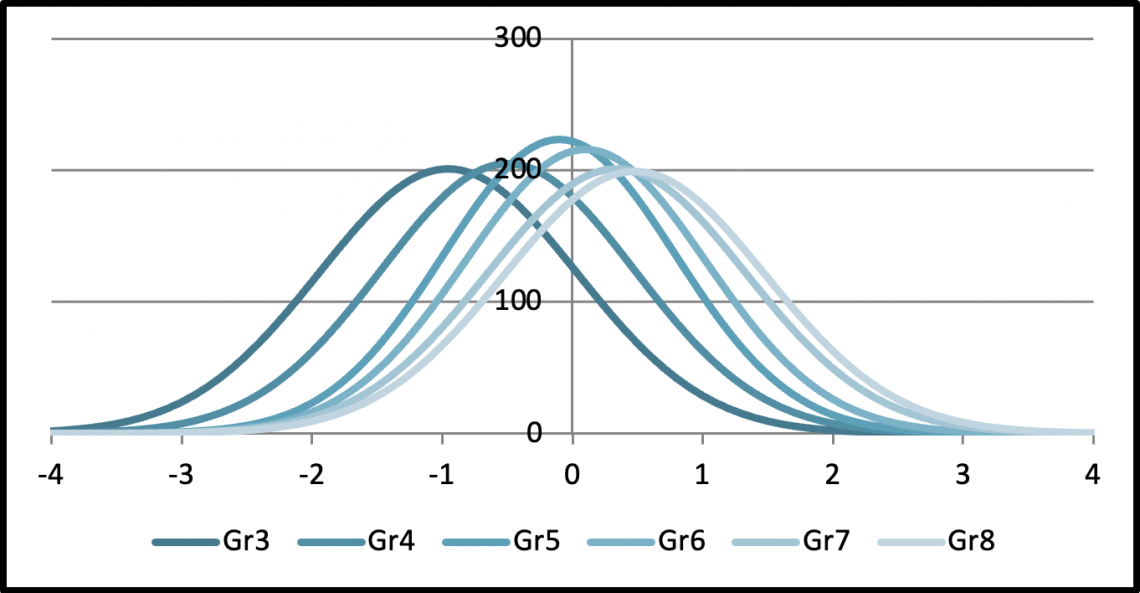
Interestingly, reverting back to the vertically scaled scores that were necessary to determine grade equivalents in the first place has not solved the problem of score overlap across grades. A score distribution for students at all grades combined would be a giant normal curve. However, a score distribution can be generated for each grade separately, but depicted in the same graph. The figure below shows a real set of such score distributions from a commercial test series.
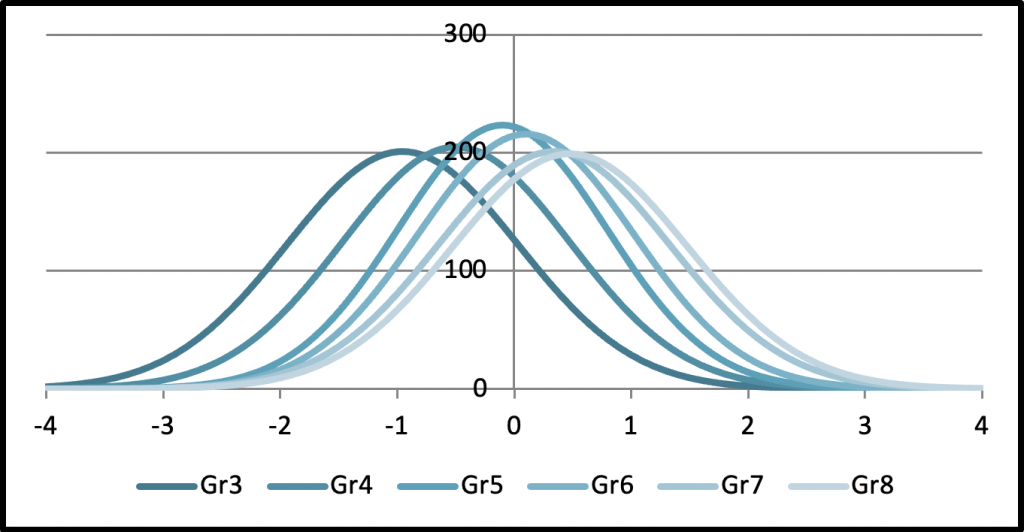
The horizontal scale is in standard deviations units, but the numbers could just as well have been 100, 200, …, 900 – a range like that being typical for vertical scales. One cannot help but notice the extreme overlap reflected in the distributions. Notice, for example, that a student doing pretty well on the third grade test has a vertical scale score somewhere well up into the range of scores for fifth graders. It’s not surprising that some testing programs, even after producing these impressive vertical scales, then transform each grade’s set of scores to a new score scale unique to that grade — e.g., 300 to 399 for third graders, 400 to 499 for fourth graders, and so on. Such transformations, of course, do not change the positions of scores within a grade level relative to one another. But only scores of students in the same grade can be subtracted and averaged meaningfully.
Interest in Growth Scores
Early in the NCLB era, it was not unusual for states to scale tests separately for each grade tested and to use the same scale at each grade – for example, a scale running from 200 to 300. The programs used a scale like this so that it wouldn’t be confused with score scales used for other familiar tests like IQ tests, ACTs, or SATs. However, I recall hearing and reading statements by policy makers that students in their students “haven’t learned a thing” when they saw average scaled scores or percentages of proficient students about the same in adjacent grades. I believe this display of assessment illiteracy contributed to increased interest in student growth. Local educators knew that on average their students “grew” a year’s worth and they wanted credit for that growth. Furthermore, schools serving high percentages of disadvantaged students could be doing a good job in terms of student growth, while their “status” scores would indicate low performance. With NCLB testing moving from two non-contiguous grades between grades 3 and 8 to all grades from 3 through 8, student growth became reasonable to compute in two subjects in several grades using state assessments. Thus, the US Department of Education began allowing the use of “growth” instead of “status” to satisfy NCLB requirements. There are many approaches to computing student growth scores, the discussion of which is beyond the scope of this post.
While individual student growth scores may not be as reliable as one would hope, average growth scores for groups of students are. That’s because the random errors associated with student-level growth scores (plusses and minuses) balance out when student growth scores are averaged. The use of schools’ average student growth for accountability purposes is reasonable. Interestingly, I can’t say the same for some ways student growth has been used for evaluating teachers. The Race to the Top requirement that student achievement weigh heavily in teacher evaluations led to misuses of average student growth, in part because the approaches pitted an individual teacher against others without taking into account the unique assignments, contexts, and supports of the individual teacher. Only a teacher’s principal or immediate supervisor can take these into account through human judgment and not a formulaic approach applied to a larger population of teachers. Nevertheless, the stakes for educators were raised considerably as a result of the Race to the Top program. Not surprisingly, this almost certainly led to the significant increase in the use of commercial or state interim testing as local educators wanted a “heads up” on their students’ likely performance on the subsequent state summative assessments. Concerns about over testing became widespread among many groups.
Academic Standards and Curricula
Student academic growth can be measured by commercial or state-provided general achievement measures. However, all would not be lost without them. One should remember that academic standards and curricula based on them are vertically articulated. In other words, growth is built into them. Student academic growth is reflected in how well the students are learning grade-specific content and skills. Teachers have to decide what is superior, adequate, and poor performance on their tests, tasks, and assignments. Those judgments are judgments about the adequacy of student growth. Mastery of grade-level material is the goal, which if reached, means adequate growth. Furthermore, teachers can learn much more about students’ individual needs from their own evidence gathering for formative purposes or from benchmark measures covering recently taught material than they can from “external” general achievement measures, which are not designed to be diagnostic. However, end-of-year summative tests can measure retention of important knowledge and skills identified in academic standards better than benchmark tests.
Conclusions
Average student growth can be useful for purposes of research, program evaluation, and accountability. And it is something that a supervisor can use with caution and good judgment in teacher evaluations along with information on other factors related to teaching effectiveness. On the other hand, individual student growth based on general achievement measures, even if the instructional period the two achievement measures span is sufficiently long, still have enough error associated with them that they should be interpreted and used conservatively. As an example, for “early warning” as described in a previous section, students targeted for additional instruction should be overidentified so that students who really need it do not miss out on it. If some who have less of a need for extra support are given it anyway, no harm is done.
Teachers, through their own testing and observations, are the ones who should know the most about the learning gaps and instructional needs of individual students. And since growth is built into the standards and curricula to which they should be teaching, their own testing should tell them which students are progressing adequately and which ones are not. Teachers are generally not surprised by the results their students achieve on commercial or state tests. Nevertheless, “external” tests (state or commercial) do provide educators and parents a perspective on what can be expected (perhaps minimally) of students at different points in their educational experience or of students in different subgroups.
If I’ve presented a seemingly negative view of growth measures, let me end this post by saying that that is not my intent. Academic growth, aka learning, is our goal in education; and imperfect as growth measures may be, there are still good uses to which they can be put. Again, average growth can be valuable for purposes of program evaluation and accountability; and “early warning” testing producing growth or status scores can be useful, provided a “no harm” principle is followed in decision making regarding individual students. Of course, both growth and status data are appropriate for inclusion in end-of-year summative assessment reports of individual student performance.