The Appeal of Computer Adaptive Testing (CAT)
Teachers and local school administrators are enamored with computer adaptive tests. They like them because they are shorter than traditional “fixed” tests (identical tests groups of students take) and because they yield immediate results. Modern test analyses by testing companies don’t lead to scores that are simply numbers of correct responses or numbers of points earned by students. The scores they produce are estimates of ability based on the difficulties of items the students answer correctly and incorrectly. Because of this, CAT doesn’t make the stronger students answer a lot of easy questions that might appear on a fixed test, and weaker students don’t have to answer a lot of hard questions that they probably can’t answer. Thus, computer adaptive tests can be shorter tests; and because they are most often made up of only machine-scorable items (e.g., multiple-choice), they can produce scores immediately after students finish their tests. The tailoring of computer adaptive tests allows the results to be more accurate for students at the very extremes of the ability continuum. Traditional fixed tests have few very easy questions and few very hard questions to differentiate among student performances at the extremes.
The Ideal Uses of CAT
Computer adaptive testing is not new. It has long been used for purposes of licensure and certification in various professions for which a total test score is the only desired outcome. CAT is designed to produce examinees total scores very efficiently. Total test scores are the focus of reporting for mandated accountability assessment programs (federal and state), which yield percentages of students at different achievement levels. (Lesson 5 and Lesson 6 dealt with such programs.) Student academic growth over the course of a school year can also satisfy accountability assessment requirements. Measures of academic growth involve total test scores and address the extent to which individual student achievement improves over time. Some districts like to gather information on student growth over periods shorter than an academic year, but too many interim tests for this purpose can be problematic if the time between administrations is so short that measurement error overshadows the limited growth that can occur. Just by chance, scores showing negative growth can result even though real positive growth had to occur.
How CAT Works
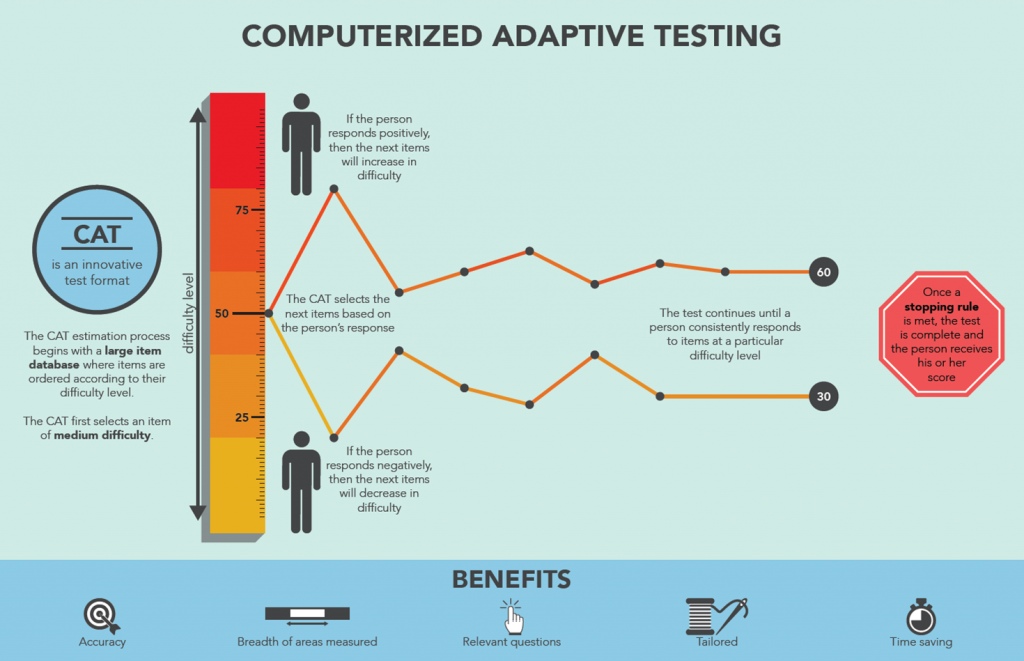
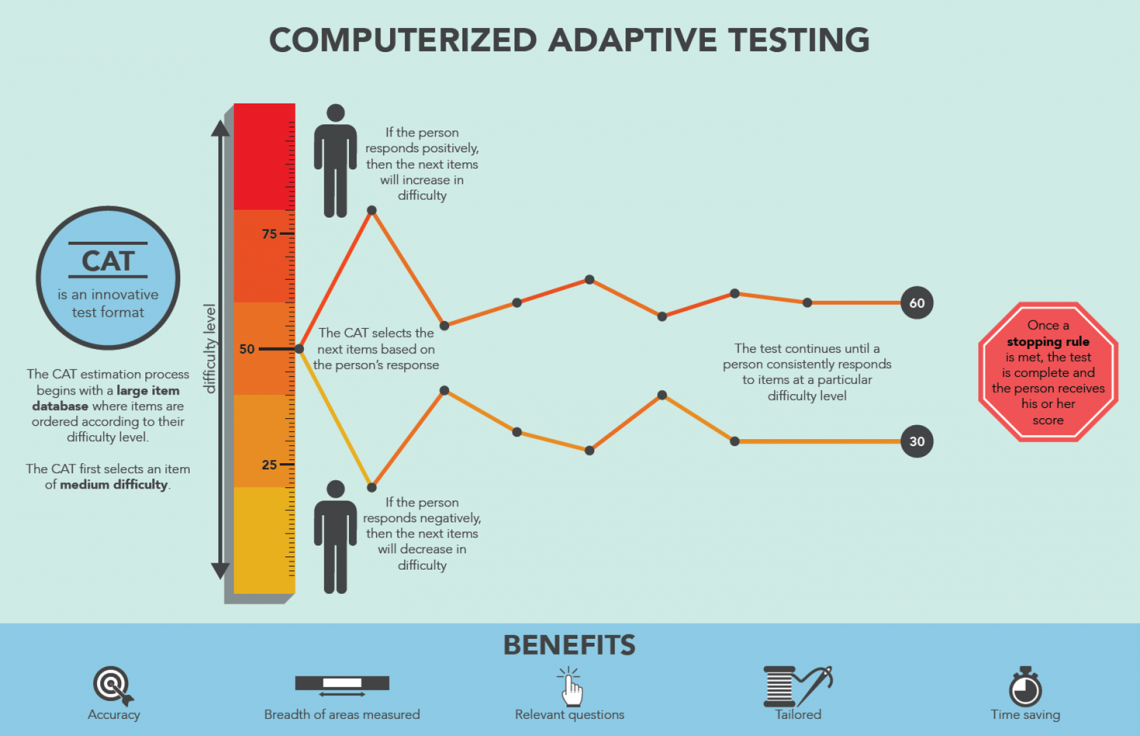
This graphic shows how CAT selects items to be administered to an individual student. The selection of an item depends on the student’s performance (correct or incorrect response) to the previous item administered. If the student answers a question correctly, the next question will be a harder question. If the student answers a question incorrectly, the next question will be an easier question. As this process continues, CAT zeroes in on an ability estimate (a total test score) for the student. The process stops according to a stopping rule which calls for the measurement error for a score to be less than a pre-determined threshold value. This process is enabled by the fact that testing experts have put examinees and items on the same scale. Or more precisely, they have put examinee scores on the same difficulty scale on which the items belong. The next section explains this.
Item Mapping
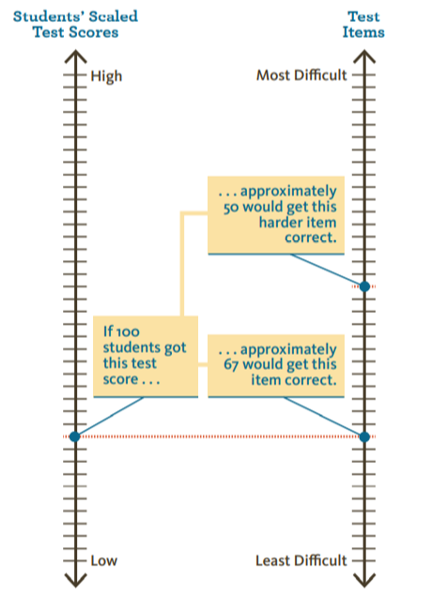
This graphic shows what it means for student scores and test items to be on the same scale. The two are “mapped” to each other. As illustrated, for a group of students scoring at a particular place on the score scale, two thirds would answer correctly (or through field testing did answer correctly) the item corresponding to that score. Of those same students, a smaller percentage would get a harder item correct, and a larger percentage would get an easier item correct.
Item Mapping: NAEP Gr. 4 Math
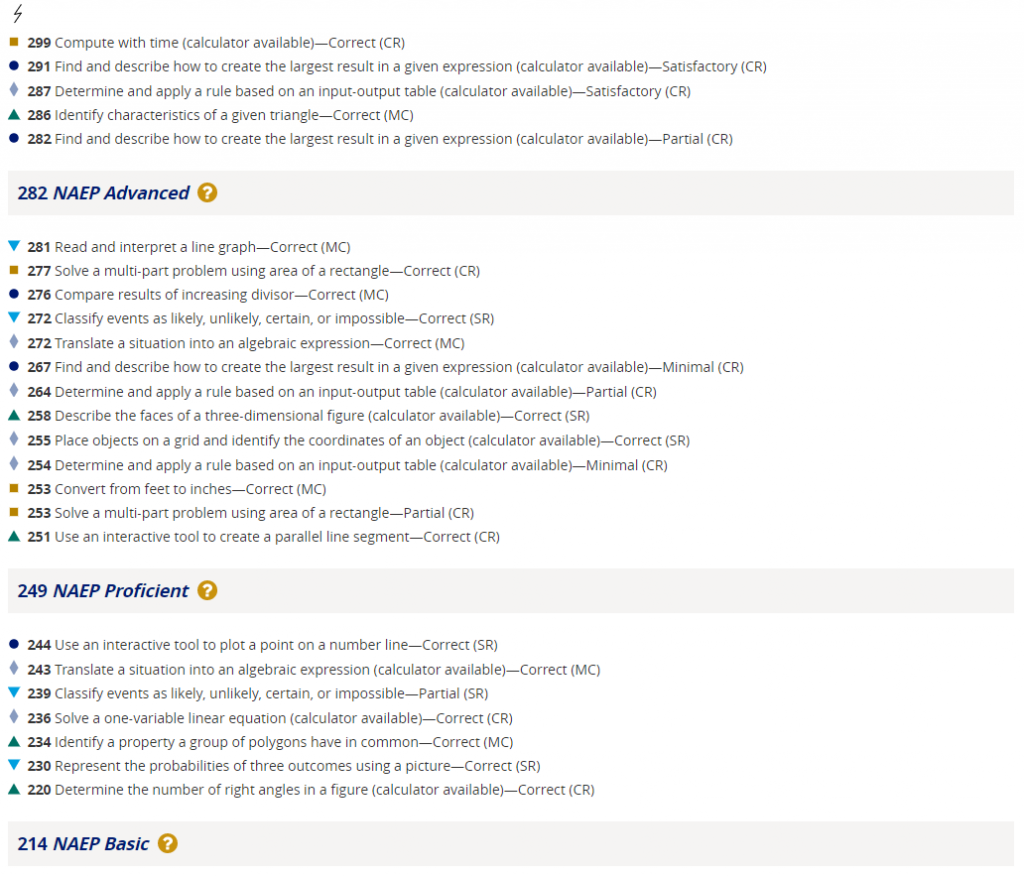
Item maps are often provided by companies doing adaptive testing, but item mapping is not solely a process associated with CAT. The National Assessment of Educational Progress has made legitimate use of item maps to give people a general sense of the abilities of students scoring at different points on the NAEP score scale. In this NAEP mapping, brief descriptions of items corresponding to different scores are shown, but not the actual items. Viewers should be careful not to overinterpret this information. As an example, the display shows that two-thirds of students scoring 236 can solve a one-variable linear equation. Really? The actual item is not shown. It could involve a very simple equation, whereas solving a more complex equation might correspond to a much higher score. Another thing viewers must keep in mind is that item maps pertain to large groups of students, not individual students. More on this is explained in the next section.
Limitation 1: Misuse of Item Mapping
Computer adaptive testing companies typically provide extensive item maps as a way of getting more information to users of CAT results. As already stated, item mapping information pertains to groups of students. There is no guarantee that a student earning a particular test score can answer a corresponding item in an item map correctly. In fact, one-third of the students earning that score would answer it incorrectly. By the way, the items in an item map are publicly released items, not the items students take for record. It would be a mistake for one to reason that it would be appropriate to teach students how to answer specific items higher up on the item difficulty scale. Large percentages of them could already answer such items correctly – fewer than 67 percent, but still sizable percentages depending on how high up the difficulty scale one goes. Furthermore, educational experts would agree that using test items as the basis for instruction is bad practice. The focus should be on the curriculum standards. Assessment expert Lorrie Shepard of the University of Colorado has written at length about “item-by-item teaching with limited instructional insight.”
Limitation 2: Low Reliability of Subtest Scores
Subtest scores from general achievement measures, fixed or adaptive, are not reliable. Recall from an earlier lesson that both reliability and content validity both rely on how well a test (or subtest) represents the domain of interest. Subtest areas are still very broad. For example, one common subtest area in mathematics is Geometry and Measurement. To think that 6 to 8 items on an adaptive test or 10 to 12 items on a fixed test are adequate coverage for educators to draw conclusions about individual students’ abilities in a subtest area would be foolish. Total tests, again, fixed or adaptive, are just long enough to yield reliable total test scores. Furthermore, computer adaptive tests are not adaptive at the subtest level. This flies in the face of the reality that students can have relative strengths and weaknesses pertaining to subtest areas. Tests adaptive at the subtest level would have to be many times longer and draw from item banks many times larger than what are already fairly large item banks.
Limitation 3: Alignment to Standards Issues
The extent to which a test is aligned with content standards it is intended to cover is an important aspect of test validity. Consider the three kinds of alignment:
- Balance of Representation – spread of items across subtest areas
- Depth of Knowledge – representation of higher-order and lower-order cognitive skills
- Range of Knowledge – coverage of knowledge and skills within a subtest area
Many CAT programs use two approaches to assuring adequate Balance of Representation. Sometimes the examinees are first administered a mini, fixed test that includes items from across the subtest areas before the test goes adaptive. Also, a constraint is placed on the computer’s item selection process – a requirement that certain numbers of questions within each subtest area be selected during the administration of the adaptive component to each student.
Additional constraints to assure appropriate Depth of Knowledge and Range of Knowledge are generally not used. The item bank required to support more constraints would have to be gigantic, and the tests would have to be considerably longer. With the exception of an initial fixed mini-component, the computer’s selection of “next items” is still base solely on item difficulty. CAT tests are mostly limited in terms of Depth of Knowledge because they typically use only multiple-choice items, which generally do not tap higher cognitive skills. The same could be said about fixed tests if they don’t use any extended constructed-response items or performance tasks. The limited number of items in a computer adaptive general achievement measure and their selection based solely on item difficulty, make if highly unlikely that such a test could match a fixed test relative to the alignment category of Range of Knowledge. Range of Knowledge is very much on humans’ minds when they are constructing fixed tests.
In Summary
- Computer adaptive testing is a good approach for applications relying primarily on total test scores.
- CAT is of limited diagnostic value at the individual student level.
- Student subtest scores from computer adaptive and fixed tests are not reliable.
- Item mapping helps exemplify the capabilities of groups of students, not individual students.
- With respect to alignment to content standards, fixed tests have an edge over computer adaptive tests.